Rate-Time and Rate-Cum curves are not identical instruments, though we often make this simplification. Rate-Time Curve Criteria include:
- Rate-Time inputs are designed to work through periods of zero production which is not possible for Rate-Cum curves as they would not be advancing on the cum curve during these periods
- Rate-Time inputs are also not coordinated to a single primary product like Rate-Cum curves
- All production curves, no matter what input method must move together in-sync as per their non-curtailed input curves
Due to the above criteria, when using Rate-Time Arrays, the multiple product (oil, gas, water etc.) curves must move forward at a single curtailment factor even if there is no single percentage factor that can be applied that will produce say 50% of the gas and 50% of the water. This drives Rate-Time curves to be run on a Cum Days basis not a Cum production basis for the product most curtailed, with any calculation deltas between cum days and cum production for a product are covered in the subsequent month calculation as addition or subtraction to the production potential.
If the behavior described above is not how you wish the calculations to proceed, then the use of Rate-Cum is available and highly encouraged and can allow for interpolation between points for smooth curves.
Click image to expand or minimize.

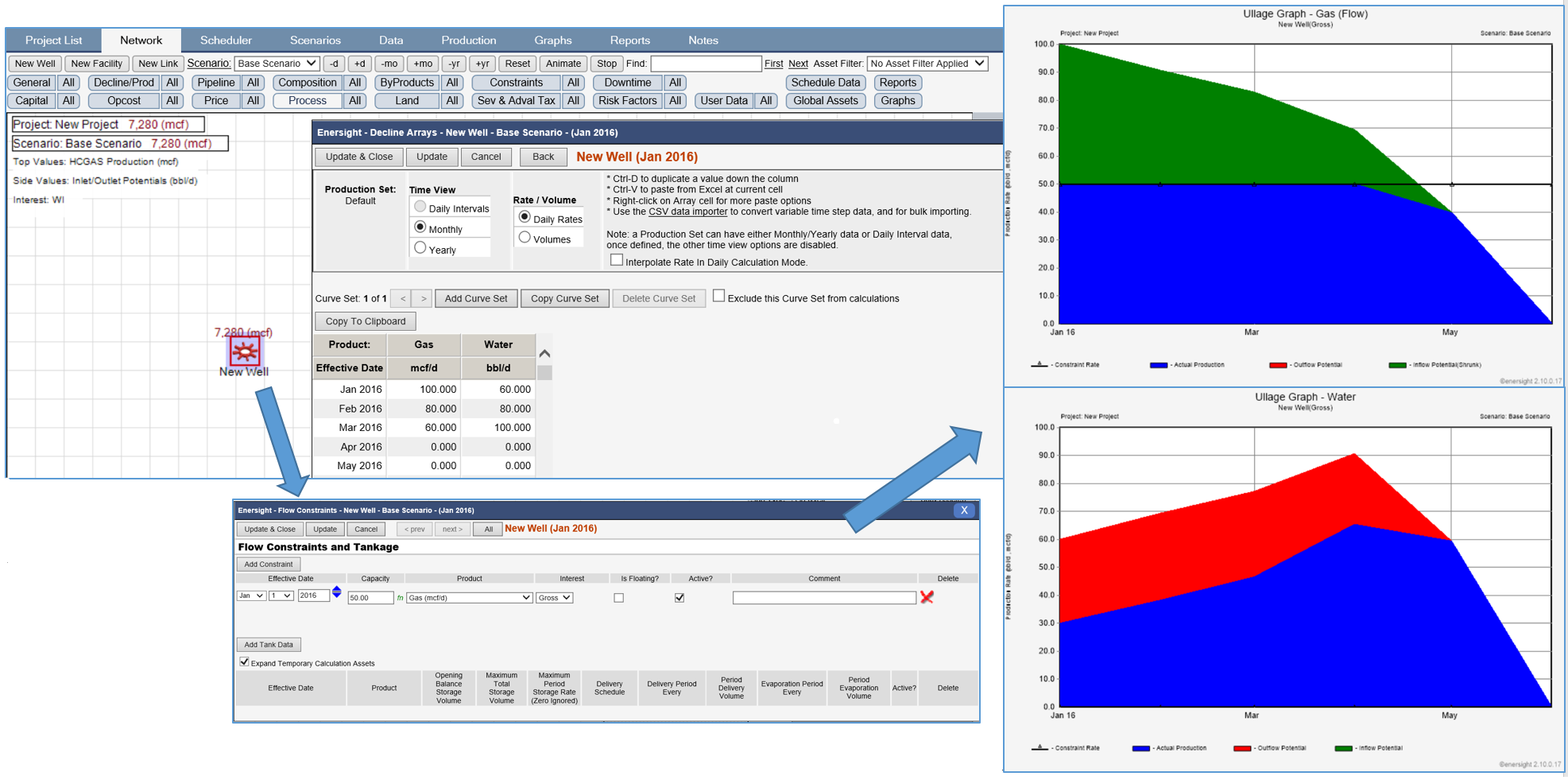
January analysis is quite straight forward:
- Potential is the first month of type curve and an equivalent 50% downtime acts due to the 50mcf/d constraint
- Both Gas and Water produce for and equivalent of 15.5 days
February’s analysis gets more complicated:
- Potential is made up of leftover production from the type curves’ first month rate plus the remaining days within the month using the type curves’ second month rate
- Gas: ((15.5 * 100) + (13.5 * 80)) / 29 = 90.69 mcf/d
- Water: ((15.5 * 60)) + (13.5 * 80)) / 29 = 69.31 bbl/d
Actual production is limited by gas constraint, which equates to differing number of days depending upon whether gas or water:
- Gas volume = 50 * 29 = 1450 mcf => 14.5 days @ 100 mcf/d i.e. it never leaves first month’s type curve rate
- Downtime Equivalent: 50 / 90.69 = 55.13% => 15.99 days
- Water volume = 55.13% * 69.31 * 29 = 1108 bbl => 17.73 days, 15.5 days at 60 bbl/d + 2.23 days at 80 bbl/d
- BUT: 14.5 days of Gas and 17.73 days of Water are not the same!
Enersight’s solution to resolve the quandary of differing production days of 14.5 for gas and 17.73 for water is to move all curves forward by the Curtailment Percentage number of days 15.99 days instead and account for the approximation in the following months as ‘extra’ production.
- For Gas: An extra 1.49 days production is shifted into March as a resultant of reconciling February: 1 day at 100 mcf/d and 0.49 days at 80 mcf/d or a total of 139.1 mcf
- For Water: A deduction of 1.74 days is shifted into March as a resultant of reconciling February for 80 mcf/d or a total of 139.1 bbl
Essentially the extra production is added to the next month’s calculation as a chunk
- This approximation holds well when the monthly changes in rate and downtime are not significant, and when we are not crossing the boundaries between data point in the calculations.
- They show a visible adjustment in the month immediately following such a transition, especially if the curtailment is then reduced to zero.
March’s analysis continues:
- Potential is made up of leftover production from the type curves’ second month rate plus the remaining days within the month using the type curves’ third month rate plus adjustments
- Gas: ((28.51 * 80) + (2.49 * 60) + 139.1) / 31 = 82.88 mcf/d
- Water: ((28.51 * 80) + (2.49 * 100) – 139.1) / 31 = 77.12 bbl/d
Actual production is limited by gas constraint, which equates to differing number of days depending upon whether gas or water:
- Gas volume = 50 * 31 = 1550 mcf
- Days = (1550 - 139.1) / 80 = 17.64 days @ 80 mcf/d once adjustments included (doesn’t need the 60 mcf/d range)
- Downtime Equivalent: 50 / 82.88 = 60.33% => 18.7 days
- Water volume = 60.33% * 77.12 * 31 = 1442.2 bbl
- Days = (1442.2 – (– 139.1)) / 80 = 19.77 days @ 80 bbl/d once adjustments included (doesn’t need the 100 mcf/d range)
